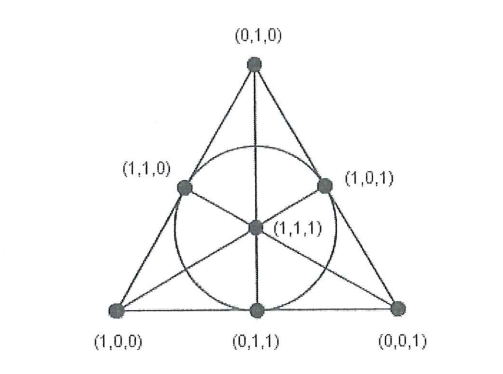
[A1] Dość przystępne wprowadzenie do geometrii afinicznej płaskiej, przy pomocy aksjomatów
Agnieszka Sołtys, "Teoria płaszczyzny afinicznej", praca magisterska, 2005. plik pdf
Geometria afiniczna to ta część zwykłej geometrii, która dotyczy
własności
punktów i prostych wyrażanych przy pomocy pojęcia równoległości,
ale bez pojęć miarowych (miar kątów, długości odcinków).
Praca dotyczy aksjomatycznego ujęcia takiej geometrii,
czyli zbudowania jej teorii poprzez oparcie się na kilku podstawowych prawach
zwanych aksjomatami.
Fascynującym aspektem geometrii afinicznej jest jej związek z algebrą.
Związek taki, jak szcegółowo omawia autorka, działa w dwie strony.
Po pierwsze, mając algebraiczną strukturę zwaną ciałem (czyli zbiór z dobrze
zachowującymi się czterema działaniami podobnymi do dodawania, odejmowania, mnożenia i dzielenia),
możemy przy jego pomocy zbudować odpowiadający mu wariant płaszczyzny afinicznej.
(Punktami są pary elementów ciała, zaś prostymi zbiory takich par stanowiące zbiory
rozwiązań równań liniowych z dwiema niewiadomymi.)
Ponieważ istnieje wiele różnych ciał, otrzymujemy w ten sposób wiele różnych waraintów
płaszczyzny afinicznej.
W drugą stronę, mając dowolną płaszczyznę afiniczną (spełniającą odpowioednie aksjomaty),
możemy w jej terminach wprowadzić na punktach dowolnej prostej działania,
które czynią z tej prostej ciało. Wszystkie te zjawiska opisane są przystępnie i dokładnie w
prezentowanej tu pracy.
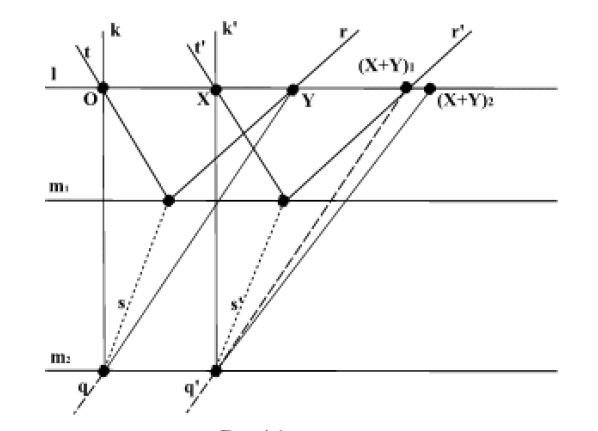
Ten schematyczny rysunek zaczerpnięty z pracy ilustruje ideę dowodu poprawności działania dodawania geometrycznie zdefiniowanego dla punktów na ustalonej prostej.