Opracowania dotyczące innych tematów geometrycznych

Opracowania z tej tematyki zamieszczam w dwóch działach.

1. Dział pierwszy zawiera prace o różnej tematyce, ale w ujęciu bardzo elementarnym,
    dostępnym także dla zainteresowanych uczniów szkół średnich:

     [E1] "Fraktale ściśle samopodobne - przykłady, wymiar fraktalny, wybrane własności"
                autorstwa Wiktorii Adamskiej, Zuzanny Narożnik i Oleny Zubets;
     [E2] "Niewspółmierność odcinków"
                autorstwa Maji Ciach, Magdaleny Mieszały i Małgorzaty Mieszały;
     [E3] "Środek ciężkości figury mierzalnej"     autorstwa Alicji Smolińskiej;
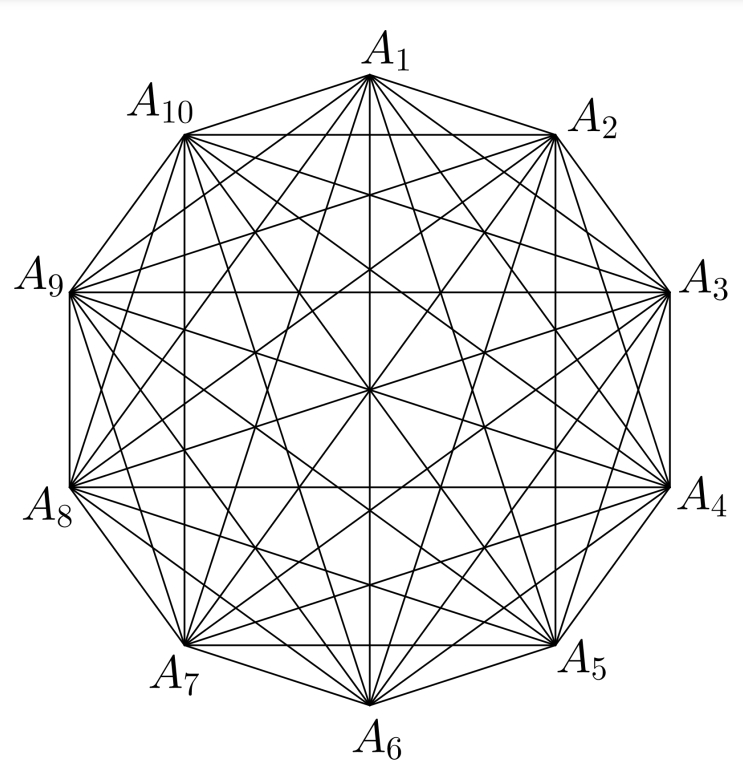
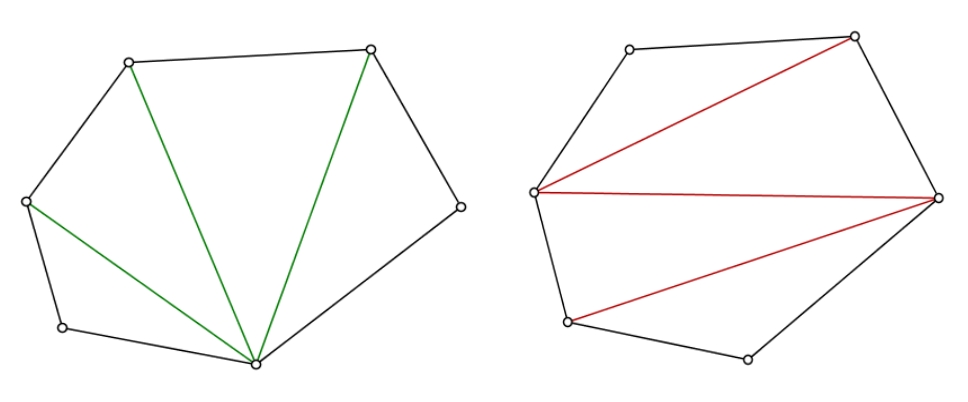
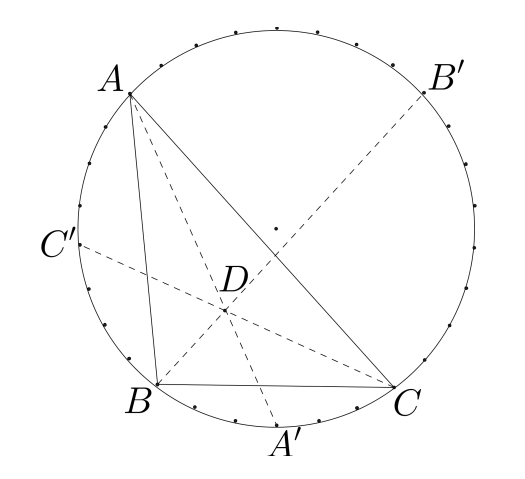
     [E4] "Liczba przecięć przekątnych w wielokącie foremnym"     autorstwa Marceliny Chodorowskiej;
     [E5] "O ilości rozwiązań zagadnienia Apoloniusza"     autorstwa Tomasza Stawickiego;
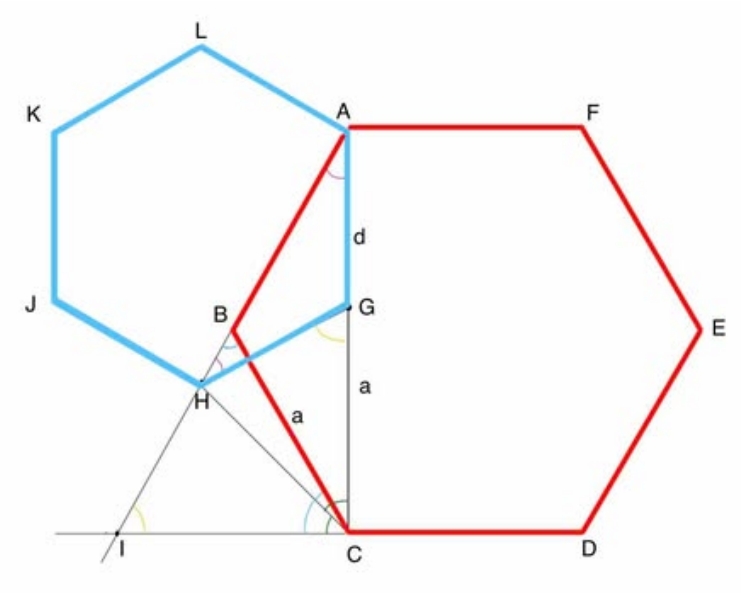
     [E6] "Konstrukcje geometryczne - skrypt do zajęć"     autorstwa Aleksandry Mierzchały.

2. Dział drugi również zawiera prace z różnej tematyki, atrakcyjne dla szerokiego kręgu odbiorców,
    ale w ujęciu nieco bardziej zaawansowanym:

     [T1] "Automorfizm zewnętrzny grupy S_6"    autorstwa Jagny Olszewskiej;
     [T2] "Klasyfikacja zwartych 2-rozmaitości teorią Morse'a"
                autorstwa Jagny Olszewskiej, Bartosza Szachniewicza i Krzysztofa Szymańskiego;
     [T3] "Teoria węzłów"    autorstwa Szymona Cygana, Bartosza Maciuraka,
                Macieja Mazurka i Remigiusza Suwalskiego.

Poniżej zamieszczam krótkie omówienia prac z tych dwóch działów.

[E1] O najprostszych fraktalach (tzw. figury ściśle samopodobne) i ich wymiarze fraktalnym

Wiktoria Adamska, Zuzanna Narożnik, Olena Zubets, "Fraktale ściśle samopodobne - przykłady, wymiar fraktalny, wybrane własności", projekt zespołowy, 2025.    plik pdf

Fraktale są obiektami wzbudzającymi dość powszechne zainteresowanie, ale niełatwo o nich mówić w sposób ścisły na poziomie elementarnym. Zamieszczona tu praca jest dość udaną próbą takiego elementarnego rozważania o fraktalach - dzięki skupieniu się na dość prostym ale ciągle bogatym i ciekawym przypadku tzw. figur ściśle samopodobnych. Figury takie posiadają rozkład na kilka części, z których każda jest pomniejszeniem całości w tej samej skali pomniejszenia. Autorki pracy prezentują dużo różnorodnych przykładów takich fraktali, co przekonuje, że figury takie można projektować i konstruować samodzielnie.
Ważnym aspektem pracy jest analiza opisywanych przykładów pod kątem ich wymiaru fraktalnego. Wymiar fraktalny jest ciekawym konceptem, uogólniającym zwyczajny wymiar. Fascynujące jest, że taki wymiar fraktalny figury nie musi być liczbą całkowitą. Autorki wyliczają wymiar fraktalny dla opisywanych w pracy przykładów, i przekonują nas, że wymiar taki może być dowolną liczbą rzeczywistą z pewnego zakresu (w przykładach z pracy jest to zakres od 0 do 2).

[E2] Niewspółmierność odcinków jako geometryczny odpowiednik niewymierności liczb,
i metody geometrycznego udowadniania niewspółmierności

Maja Ciach, Magdalena Mieszała, Małgorzata Mieszała, "Niewspółmierność odcinków", projekt zespołowy, 2025.
plik pdf

Niewspółmierność odcinków jest geometrycznym odpowiednikiem faktu, że stosunek ich długości jest liczbą niewymierną. Niewspółmierność oznacza, że nie istnieje mniejszy odcinek, który mieściłby się calkowitą liczbę razy w obu wyjściowych odscinkach (odcinki te "nie mają wspólnej miary"). Związek tego pojęcia z ideą niewymierności liczby jest starannie wyjaśniony w pracy.

Pierwszy dowód istnienia liczb niewymiernych (przedstawiony przez uczniów Pitagorasa) był w istocie dowodem niespółmierności boku kwadratu i jego przekątnej (odpowiada to niewymierności liczby pierwiastek z 2). Dowód ten miał charakter czysto geometryczny, i nie zawierał żadnych argumentów o charakterze arytmetycznym, jakich współcześnie używa się w dowodach niewymierności. Od tego czasu powstało kilka innych pomysłów na geometryczne dowodzenie niewspółmierności różnych par odcinków.

W pracy omówione są trzy różne serie przykładów odcinków niewspółmiernych, wraz z przystępnymi dowodami ich niewspółmierności. Niektóre z tych przykładów są bardzo oryginalne, gdyż żadnych ich odpowiedników nie udało się znaleźć w dostępnych źródłach. Wszystkie argumenty w pracy wsparte są licznymi pomocnymi rysunkami.

[E3] Elementarne i ścisłe wprowadzenie pojęcia środka ciężkości figury na płaszczyźnie

Alicja Smolińska, "Środek ciężkości figury mierzalnej", praca magisterska, 2013.    plik pdf

Pojęcie środka ciężkości figury jest zwykle używane intuicyjnie, przez odwołanie do "fizykalnej" intuicji. Jego matematyczna formalizacja kojarzona jest najczęściej z pojęciem całkowania, i jako taka jest dość zaawansowana.

Celem zamieszczonej tu pracy jest ścisłe i w miarę elementarne podejście do pojęcia środka ciężkości figur na płaszczyźnie. W pracy kolejno omówione są następujące zagadnienia: środek ciężkości skończonego układu punktów z wagami, środek ciężkości trójkąta i jego nieoczywiste własności, środek ciężkości wielokąta, i na koniec środek ciężkości figury mierzalnej w sensie Jordana. Tylko to ostatnie zagadnienie wymaga pewnej wiedzy spoza zakresu szkoły średniej - mianowicie o zbieżności i granicach ciągów. Podejście do wcześniejszych zagadnień nie wymaga zaawansowanych pojęć.

[E4] Trudne pytanie o liczbę punktów wewnątrz wielokąta foremnego,
w których przecinają się jego przekątne

Marcelina Chodorowska, "Liczba przecięć przekąt nych w wielokącie foremnym",
praca licencjacka, 2016.    plik pdf

Dość łatwo jest obliczyć liczbę takich par przekątnych w n-kącie foremnym, które przecinają się wewnątrz tego wielokąta. Ta liczba nie jest jednak tą liczbą, która występuje w tytule pracy, gdyż w niektórych punktach mogą się przecinać ze sobą więcej niż dwie przekątne. Tak więc powyższa liczba par przekątnych jest tylko oszacowaniem górnym na szukaną liczbę punktów przecięcia. Wyznaczenie dokładnej liczby punktó przecięcia przekątnych w n-kącie foremnym, dla dowolnego n, nie jest łatwe.
Praca zawiera kilka nie całkiem łatwych, ale jednak przystępnych, obserwacji umożliwiających znacznie lepsze oszacowanie szukanej liczby punktów przecięcia niż oszacowanie wspomniane powyżej.

Rysunek obok reprezentuje przedstawioną w pracy analizę typowych przypadków, gdy trzy przekątne wielokąta foremnego przecinają się w jednym punkcie. Uwzględnienie takich trójek przekątnych, wraz z kilkoma innymi nietrudnymi obserwacjami, pozwala uzyskać bardzo dobre oszacowanie szukanej liczby punktów przecięcia przekątnych.

[E5] Ile jest okręgów, które są styczne do każdego z trzech zadanych okręgów?

Tomasz Stawicki, "O ilości rozwiązań zagadnienia Apoloniusza", praca magisterska, 2001.    plik pdf

Zagadnienie Apoloniusza brzmi następująco: mając dane trzy dowolne okręgi, skonstruuj okrąg który jest styczy do każdego z tych trzech okręgów. Każdy taki skonstruowany okrąg jest wtedy nazywany okręgiem Apoloniusza. W Rozdziale 1 pracy autor opisuje konstrukcję okręgu Apoloniusza (za pomocą cyrkla i linijki).
Jednak głównym celem pracy jest nie sama konstrukcja, a raczej pytanie o liczbę rozwiązań zagadnienie, czyli liczbę okręgów stycznych do każdego z trzech zadanych okręgów. Okazuje się, że liczba tych rozwiązań może być różna, w zależności od wzajemnego położenia trzech zadanych okręgów. W Rozdziale 2 pracy autor przeprowadza rozległy eksperyment numeryczny znajdując liczbę rozwiązań w kilkudziesięciu zróżnicowanych przykładach. Okazuje się, że liczba rozwiązań w tych przykładach waha się od zera do ośmiu. Wszystko to jest zilustrowane numerycznie generowanymi rysunkami, których kolekcja stanowi bardzo ciekawą wizualnie część pracy.
W Rozdziale 3 autor podejmuje teoretyczną analizę liczby rozwiązań. Jego podejście opiera się na obserwacji, że każdy szukany okrąg zawiera się w jednym z obszarów, na ktoóre dzielą płaszczyznę trzy zadane wyjściowe okręgi. Autor klasyfikuje typy takich możliwych obszarów, a następnie dla każdego typu obszaru wyznacza liczbę szukanych okręgó wewnątrz tego obszaru. Ta część pracy pozwala, dla dowolnej konfiguracji trzech wyjściowych okręgów, ustalić szybko łączną liczbę rozwiązań.
W ostatnim czwartym rozdziale pracy autor przytacza (w sposób bardzo przystępny) znany algebraiczny dowód faktu, że rozwiązań zagadnienia Apoloniusza nie może być nigdy łącznie więcej niż 8.

[E6] Przystępne wprowadzenie do matematycznej teorii konstrukcji geometrycznych

Aleksandra Mierzchała, "Konstrukcje geometryczne - skrypt do zajęć", praca magisterska, 2004.    plik pdf

Choć zagadnienie konstrukcji cyrklem i linijką należy do geometrii, jego matematyczna analiza i teoria ma charakter algebraiczny, i wiąże się z problemem rozwiązywania równań algebraicznych. Ten właśnie związek omawiany jest w bardzo przystępny sposób w zamieszczonym tu skrypcie (jest to nazywane metodą algebraiczną w konstrukcjach geometrycznych).
W skrypcie omówione jest pojęcie liczb konstruowalnych (z grubsza, liczb będących długościami odcinków dających się skonstruować za pomocą cyrkla i linijki, wychodząc od zadanego odcinka długości 1). Wyjaśnione jest też jak sprowadzić pytanie o wykonalność jakiejś konstrukcji do pytania o konstruowalność pewnej liczby związanej z tą konstrukcją. W przypadku klasycznych zagadnień trysekcji kąta i podwojenia sześcianu sprowadza się to do pytania o konstruowalność rozwiązań pewnych równań algebraicznych stopnia 3. W skrypcie starannie uzasadniona jest niekonstruowalność rozwiązań tych odpowiednich równań, skąd wynika niewykonalność obu tych konstrukcji.
Analiza związana z konstrukcjami geometrycznymi prowadzi też do algebraicznego pjęcia liczb algebraicznych, i ich stopnia, także przytępnie omówionego w skrypcie. Swoego rodzaju kulminacją jest rozwiązanie problemu konstruowalności poszczególnych wielokątów foremnych.
W skrypcie znajdują się też liczne ćwiczenia i zadania do samodzielnego rozwiązania.

[T1] O pięknej unikalnej własności grupy permutacji 6 elementów,
i jej kombinatorycznym wyjaśnieniu

Jagna Olszewska, "Automorfizm zewnętrzny grupy S_6", praca licencjacka/seminaryjna, 2025.    plik pdf

Automorfizm to takie wzajemnie jednoznaczne przyporządkowanie elementom grupy innych elementów tej samej grupy by zachowane było grupowe działanie (iloczyn), tzn. by iloczyn obrazów dwóch elementów był zawsze tym samym co obraz ich iloczynu. Najprostsze automorfizmy grup permutacji odpowiadają przenumerowaniu permutowanych elementów, i takie automorfizmy nazywają się wenętrznymi. Interesującym nas pytaniem jest: czy grupa permutacji posiada jakikolwiek automorfizm, który nie jest wewnętrzny.
Okazuje się, że jedyną grupą permutacji, która ma taki nie-wewnętrzny automorfizm jest grupa permutacji sześciu elementów, tu oznaczana jako S_6. W dodatku, z dokładnością do przenumerowania permutowanych elementów taki automorfizm nie-wewnętrzny jest jedyny.
Celem pracy jest przytoczenie dowodów tych własności, ale przede wszystkim jakieś sensowne opisanie tego jedynego automorfizmu nie-wenętrznego. Okazuje się, że taki opis jest możliwy, i to na kilka różnych sposobów, a sensowność takiego opisu polega na kombinatorycznej interpretacji opisywanego automorfizmu. Taka interpretacja polega na tym, że z sześciu elementów tworzymy wszystkie możliwe kombinatoryczne konfiguracje pewnego rodzaju, których jest także sześć, zaś każda permutacja wyjściowych sześciu elementów zamienia dowolną taką konfigurację w inną, dając w ten sposób permutację tych sześciu konfiguracji. Autorka przytacza taką piękną kombinatoryczną interpretację opracowaną właściwie samodzielnie, i różniącą się od interpretacji wsześniej przytaczanych w literaturze. Oczywiście na końcu okazuje się, że jest to ten sam (jedyny) nie-wewnętrzny automorfizm.

Zjawisko węzła nie jest łatwe do sensownego ujęcia matematycznego. Kiedy już się to zrobi, to jeszcze trudniejsze jest klasyfikowanie węzłów, np. uzasadnianie że dwa węzły istotnie różnią się od siebie. Oba te zagadnienia omówione są w dość przystępny sposób w przedstawionej pracy.
Pojęcie węzła wprowadzone jest za pomocą łamanych zamkniętych bez samoprzecięć (w przestrzeni), z dokładnością do modyfikacji polegających na poruszaniu łamanej (cały czas unikając samoprzecięć) lub dzieleniu i zaginaniu niektórych jej segmentów.
Dla rozróżniania węzłów przydatne okazuje się opisanie ich za pomocą tzw. diagramu (jak na rysunku obok), oraz ustalenie kiedy dwa diagramy reprezentują ten sam węzeł. Diagramy można potem wykorzystać do znajdowania tzw. niezmienników węzłów, czyli pewnych "cech" dających się wyczytać z diagramu, które nie ulegają zmianie gdy diagram zastąpi się innym diagramem reprezentującym ten sam węzeł. W pracy opisanych jest kilka takich niezmienników, związanych np. z ideą kolorowania diagramów, lub z ideą przypisywania diagramom pewnych macierzy lub wielomianów.