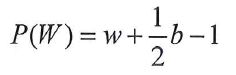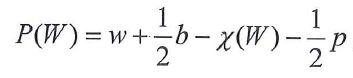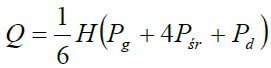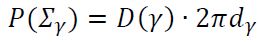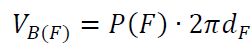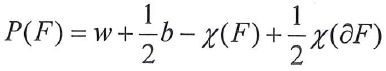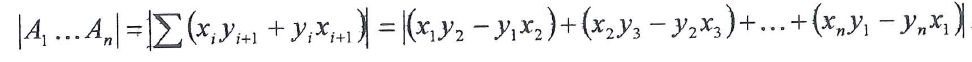Dział 1:
Ciekawe wzory na pole i objętość
W opracowaniach zamieszczonych w tym dziale możecie poznać rozmaite mało znane wzory
na pole i objętość, takie jak na przykład widniejące poniżej, po prawej stronie.
[W1] Wielokąty o wierzchołkach w punktach kratowych i wzór na ich pole
Lidia Gniadkowska, "Wzór Picka dla figur wielokątnych", praca magisterska, 2000.
plik pdf
W pracy zaprezentowany zostanie (i udowodniony) ciekawy wzór na pole wielokątów,
których wszystkie wierzchołki są tzw. punktami kratowymi, czyli punktami
o obu współrzędnych całkowitych w ustalonym układzie kartezjańskim (o takich punktach
można też myśleć jak o punktach węzłowych na papierze w kratkę, w którym rozmiar
podstawowego kwadracika wynosi 1x1). Wzór wyraża pole wielokąta za pomocą liczby
punktów kratowych znajdujących się we wnętrzu oraz na brzegu tego wielokąta.
Znany jest w literaturze pod nazwą wzór Picka, od nazwiska odkrywcy.
W drugiej części pracy wzór ten jest uogólniony w taki sposób, by wyliczał pole
dla dużo bardziej skomplikowanych figur, nazywanych figurami wielokątnymi,
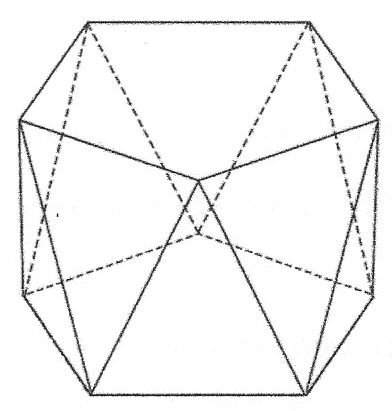
takich jak np. na rysunku obok, oczywiście dalej przy założeniu, że wszystkie
wierzchołki figury są punktami kratowymi.
|
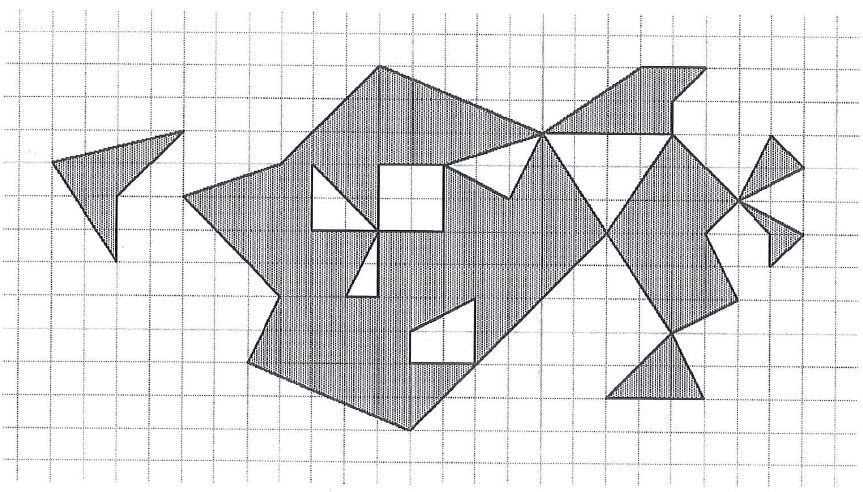
przykład figury wielokątnej o wierzchołkach kratowych
|
[W2] Wzory na objętość i pole powierzchni brył obrotowych
Paulina Haręża, "Elementarny dowód twierdzeń Pappusa-Guldina", praca magisterska, 2016.
plik pdf
|
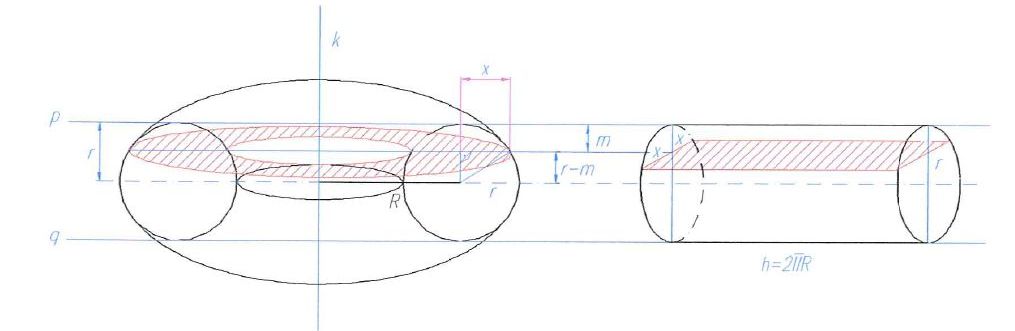
Bryłę obrotową można poglądowo traktować jak kawałek pręta o ustalonym kształcie przekroju
wygiętego w taki sposób, że jego jeden koniec spotyka się z drugim. Przykład takiej bryły,
o przekroju kołowym, pokazany jest na rysunku poniżej.
Pierwszy z wzorów Pappusa-Guldina mówi, że objętość takiego "wygiętego pręta" jest równa
iloczynowi jego długości oraz pola przekroju, gdzie przez długość rozumie się długość okręgu
jaki zatacza środek ciężkości figury płaskiej będącej przekrojem. Pomimo poglądowej
"oczywistości" wzór ten wcale nie jest łatwy do wyprowadzenia elementarnymi metodami.
Takie właśnie wyprowadzenie tego wzoru znajdzie czytelnik w przedstawianej pracy.
|
|
Rysunek powyżej ilustruje jeden z kroków wyprowadzenia wzorów Pappusa-Guldina,
zgodnie ze sposobem przedstawionym w pracy.
|
[W3] O bardzo uniwersalnym wzorze na objętość brył
Magdalena Gapska, "Objętość brył, których funkcja pola przekroju jest wielomianem conajwyżej trzeciego stopnia",
praca magisterska, 2005.
plik pdf
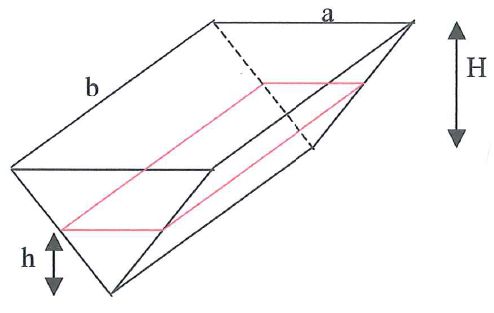
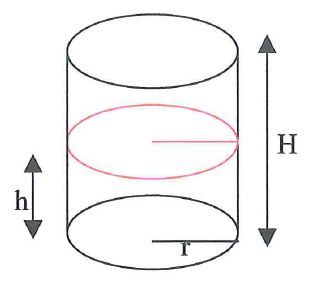
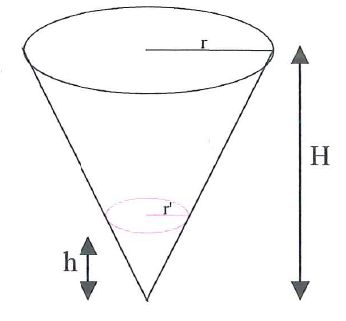
Z tej pracy dowiecie się, że istnieje uniwersalny wzór, wyglądający następująco
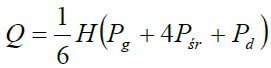
przy pomocy którego daje się wyznaczyć objętość mnóstwa różnych brył, a wśród nich:
graniastosłupów, walców, stożków, stożków ścietych, ostrosłupów, kuli i jej wycinków,
paraboloid i hiperboloid obrotowych, i wielu innych.
Cechą wspólną tych wszystkich brył, decydującą o prawdziwości wzoru w ich przypadku,
jest posiadanie tzw. funkcji pola przekroju będącej wielomianem stopnia conajwyżej 3.
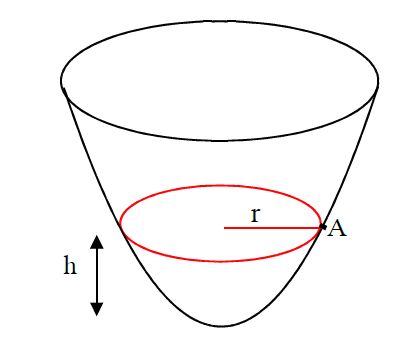
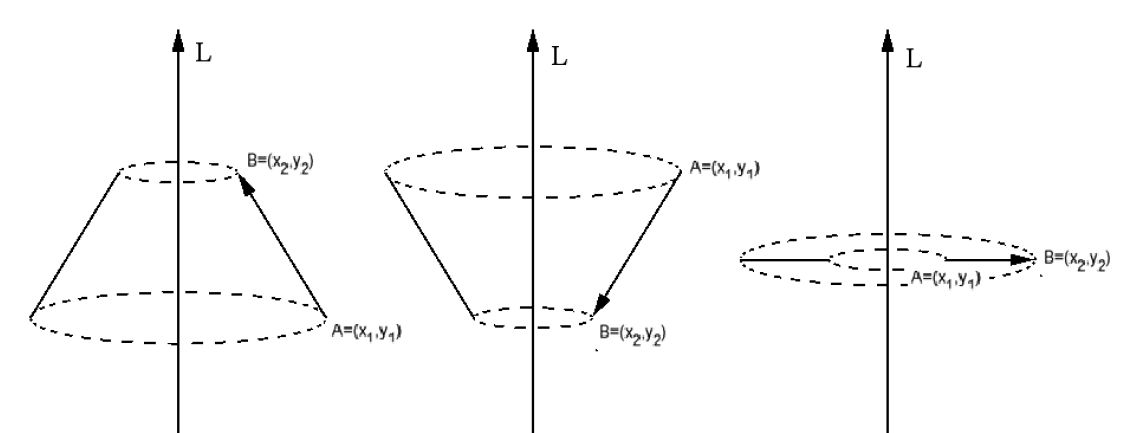
Funkcja pola przekroju reprezentuje sposób, w jaki zmienia się pole przekroju bryły w zależności od wysokości
h poziomej płaszczyzny przekroju.
Na rysunku obok pokazane są bryły o funkcjach pola przekroju stałej, liniowej i kwadratowej.
|
|
|
[W4] Uniwersalny wzór na pole wielokąta w układzie współrzędnych
(i nie tylko)
Agnieszka Burska, "Zorientowane pole wielokątów", praca magisterska, 2001.
plik pdf
"Bohaterem" tej pracy jest pojęcie zorientowanego pola, które jest
w zasadzie zwykłym polem, jednak ze znakiem zależnym od wybranej orientacji obiegu
figury naokoło, po jej obwodzie. Okazuje się, co jest wytłumaczone w pracy, że
w układzie współrzędnych jest bardziej naturalne obliczenie zorientowanego pola
wielokąta niż jego zwykłago pola. Ma to ciekawe konsekwencje. Przykładowo, bez rysunku,
na podstawie samych tylko współrzędnych punktów A, B, C, D, możemy rachunkowo
rozpoznać, czy punkty C i D leżą po tej samej stronie, czy po różnych stronach
prostej AB. Podobnie można samymi tylko rachunkami ustalić, czy punkt D
leży we wnętrzu trójkąta ABC, czy nie.
Najsubtelniejsze z zaprezentowanych w pracy zastosowań pojęcia zorientowanego pola
pozwala w ścisły sposób zdefiniować pojęcie pola dla wielokątów. Odsyłam czytelnika zainteresowanego
tym aspektem do zapoznania się z Rozdziałem 4 pracy (po uprzednim zapoznaiu się także
z podstawowym Rozdziałem 1).
Dodatkową ciekawostką jest omówienie mało znanego pjęcia pola dla wielokątów gwiaździstych,
czyli wielokątów, które są "ograniczone" łamanymi zamkniętymi z samoprzecięciami.
Tu odsyłam czytelników do Rozdziału 6 w pracy.
|
|
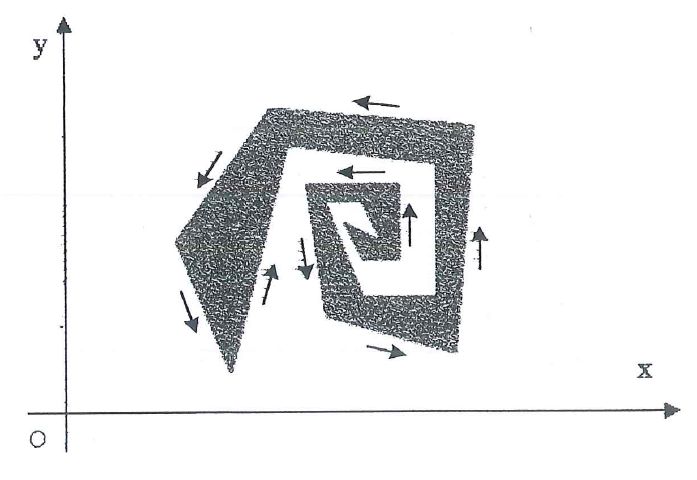
wyprowadzonym w tej pracy wzorem można obliczyć pole dowolnego wielokąta, o ile znamy
współrzędne jego kolejnych wierzchołków
|
Dział 2:
Ścisłe podstawy teoretyczne pojęcia pola wielokątów i objętości wielościanów
Opracowania [T1], [T2] i [T3] pozwalają zapoznać się w elementarny sposób z tym jak intuicyjne
pojęcia pola i objętości ujmowane są w sposób ścisły przez matematyczne teorie
datyczące tych konceptów.
Praca [T1] podejmuje problem jak
w sposób ścisły zdefiniować liczby oznaczające pole wybranego wielokąta lub objętość
wybranego wielościanu, i jak przy tym mieć pewność, że liczby te zostały przypisane
w sposób jednoznaczny. Nie jest to proste, a sposób zaprezentowany w pracy jest
wprawdzie pracochłonny, ale za to całkowicie elementarny. Sposób ten w szczególności
nie korzysta z pojęcia granicy ciągu, jak to się dzieje w przypadku innych sposobów
popularnych w matematyce teoretycznej.
W pracy [T2] przedstawione jest
w przystępny sposób aksjomatyczno-dedukcyjne podejście do objętości.
Teoria taka polega na przyjęciu czterech podstawowych bardzo naturalnych założeń,
zwanych aksjomatami teorii objętości, oraz na wyprowadzaniu wszystkich
pozostałych własności i wzorów ścisłym logicznym wnioskowaniem. Oprucz przedstawienia
samej teorii, w formie logicznego wyprowadzania kolejnych wniosków z aksjomatów,
praca zawiera też elementarny dowód niesprzeczności tej teorii, a więc jej sensowności
z logicznego punktu widzenia. Praca zawiera też dowód niezależności wszystkich
aksjomatów, czyli faktu że teoria nie może się obejść bez któregokolwiek z nich.
Opracowanie [T3]
powraca do pojęcia pola. Jest ono gruntowną analizą roli aksjomatu monotoniczności
w logicznej strukturze tej teorii.
|
|
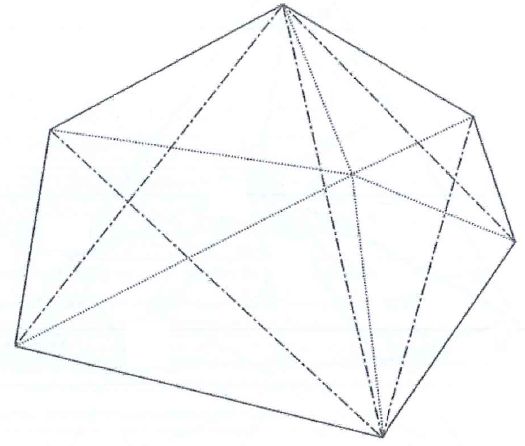
dwa naniesione na siebie podziały wielokąta na trójkąty;
definiując pole wielokąta korzysta się z jego podziału na trójkąty,
zaś kluczowym problemem jest niezależność zdefiniowanej wielkości od sposobu podziału
|
[T1] Pole i objętość bez tajemnic
Magdalena Dukiewicz,
"O pewnym sposobie ścisłego wprowadzenia pola dla wielokątów i objętości dla wielościanów", praca magisterska, 2005.
plik pdf
Jak oblicza się pole trójkąta? Ze wzoru P=ah/2. A jak wyznacza się pole dowolnego wielokąta?
Rozkładając go na trójkąty, i sumując pola tych trójkątów. A skąd wiadomo, że wynik nie zależy
od sposobu podziału na trójkąty? Na to pytanie odpowiada właśnie ta praca. Można ją też potraktować jak
ścisłe wprowadzenie pojęcia pola dla wielokątów.
W drugiej części pracy adresowany (i rozwiązany!) jest analogiczny problem dla wielościanów,
ich rozkładów na czworościany, i wyznaczania ich objętości. O ile w pierwszej części rozumowanie
jest oparte na dzieleniu wielokątów na trapezy, o tyle w drugiej rolę trapezów pełnią bryły
zwane pryzmatoidami, które można traktować jako 3D-odpowiedniki trapezów.
|
|
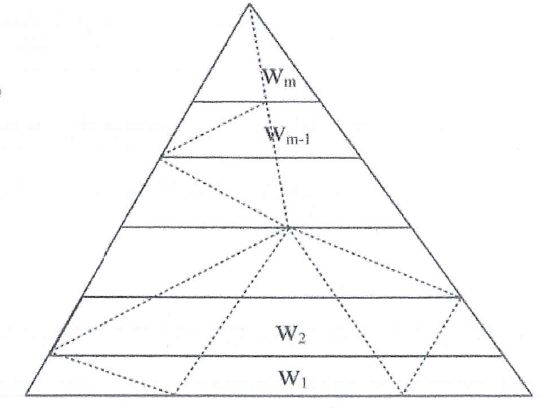
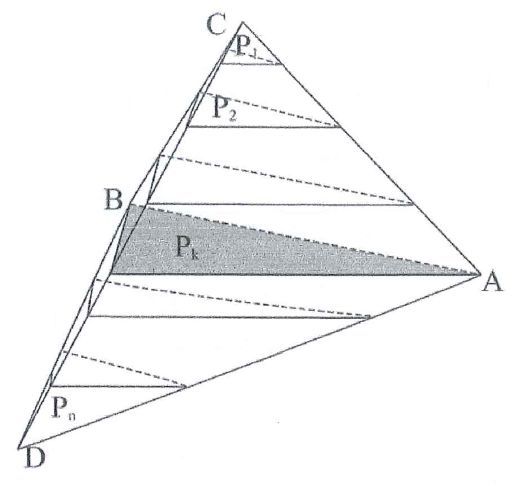
tego rodzaju podziały trójkątów na trapezy i czworościanów na pryzmatoidy
odgrywają kluczową rolę w ścisłym zdefiniowaniu pojęć
pola i objętości dla wielokątów i wielościanów
metodą opisaną w pracy
|
[T2] Teoria objętości dla wielościanów - ujęcie aksjomatyczno-dedukcyjne
Katarzyna Kowalczuk,
"Od aksjomatów objętości do wzorów na objetości wielościanów", praca magisterska, 2005.
plik pdf
Praca zawiera przystępny opis matematycznej teorii objętości dla wielościanów.
Teoria ta oparta jest na czterech prostych podstawowych zasadach, zwanych aksjomatami.
Aksjomat przystawania mówi, że przystające bryły mają jednakowe objętości.
Aksjomat sumy stwierdza, że bryła podzielona na dwie części ma objętość równą
sumie objętości tych części. Aksjomat montoniczności orzeka, że bryłą zawarta w drugiej
bryle nie może mieć objętości większej niż ta druga bryła. I wreszcie aksjomat jednostki
stwierdza, że pewien ustalony sześcian o bokach długości 1 ma objętość równą 1
(ten sześcian możemy uwarzać za nasz wzorzec objętości).
Praca składa się z trzech części. W części pierwszej pokazane jest jak można z tych czterech
aksjomatów wydedukować wszystkie podstawowe własności objętości, w tym wszystkie podstawowe szkolne
wzory na objętości brył. Część druga poświęcona jest udowodnieniu, że aksjomaty teorii objętości
nie są ze sobą sprzeczne, czyli że nie mogą doprowadzić nas do logicznych absurdów. Część trzecia
poświęcona jest problemowi niezależności poszczególnych aksjomatów, czyli uzasadnieniu tego,
że każdy z aksjomatów jest niezbędny, bo bez niego pewnych własności nie dołoby się wyprowadzić.
|
|
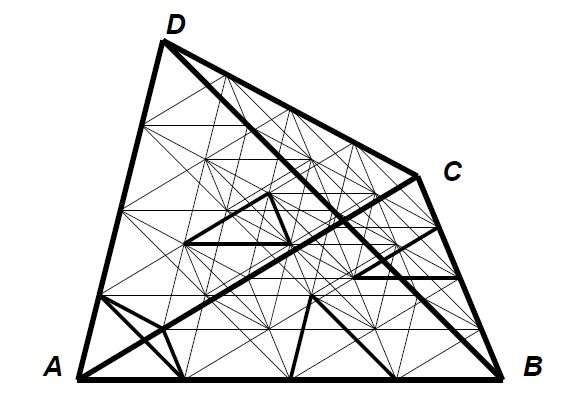
analiza podziałów czworościanu na mniejsze czworościany
stanowi ważny element w dowodzie, że teoria objętości dla wielościanów
jest niesprzeczna
|
[T3] Czego nie da się wydedukować bez korzystania z zasady, że pole wzrasta wraz
z powiększaniem się figury?
Teresa Majcher,
"Aksjomat monotoniczności w teorii pola figur wielokątnych", praca magisterska, 2005.
plik pdf
Matematyczna teoria pola dla figur na płaszczyźnie oparta jest na czterech prostych zasadach,
zwanych aksjomatami. Z tych czterech aksjomatów można metodą rozumowania dedukcyjnego
wyprowadzić wszystkie fakty dotyczące pola, w tym wszystkie wzory na pole figur. Jednym
z aksjomatów jest reguła mówiąca, że pole figury zawartej w drugiej figurze nie może być
większe niż pole tej drugiej figury. Jest to tzw. aksjomat monotoniczności.
Opisywana tu praca podejmuje problem, na ile aksjomat montoniczności jest istotny,
i czy bez niego nie da się równie dobrze wyprowadzić wszystkich własności pola. Odpowiedź jest
negatywna, natomiast z analizy przeprowadzonej w pracy możemy się dowiedzieć także gdzie przebiega
granica pomiędzy tym, co można udowodnić bez tego aksjomatu, a tym czego udowodnić się
już nie da.
Dział 3: Metoda niepodzielnych i zasada Cavalieriego, czyli jak całkowano przed wynalezieniem całki
Jak "wysumować" bryłę zapełniającymi ją płaskimi przekrojami za pomocą równoległych płaszczyzn?
Albo jak wysumować figurę zapełniającymi ją liniami? Czy do takiego "sumowania" stosują się
jakieś algebraiczne reguły? Czy można ich użyć do wyliczeń objętości brył albo pól figur i powierzchni?
Są to pytania nurtujące uczonych u schyłku średniowiecza i początku ery nowożytnej,
zaś próby odpowiedzi na nie znane są pod nazwą teorii niepodzielnych. Podobne rozważania
prowadził zresztą już w starożytności Archimedes, uzyskując dzięki nim kilka ciekawych rezultatów,
np. wyliczenie objętości kuli (patrz rysunek poniżej).
Metoda niepodzielnych nie wymaga zaawansowanej abstrakcji, głeboko przemawia do wyobraźni,
ale ma charakter bardziej poglądowy niż ścisły. Jej fragmentom można jednak nadać zupełnie
precyzyjny charakter, a jej zastosowania są całkiem liczne i dają rezultaty spektakularne,
niemożliwe chyba do uzyskania inną poglądową i elementarną metodą. Poniższe opracowania
w tym dziale prezentują rozmaite ścisłe warianty metody niepodzielnych, oraz wiele
niebanalnych wyliczeń dokonanych przy ich pomocy.
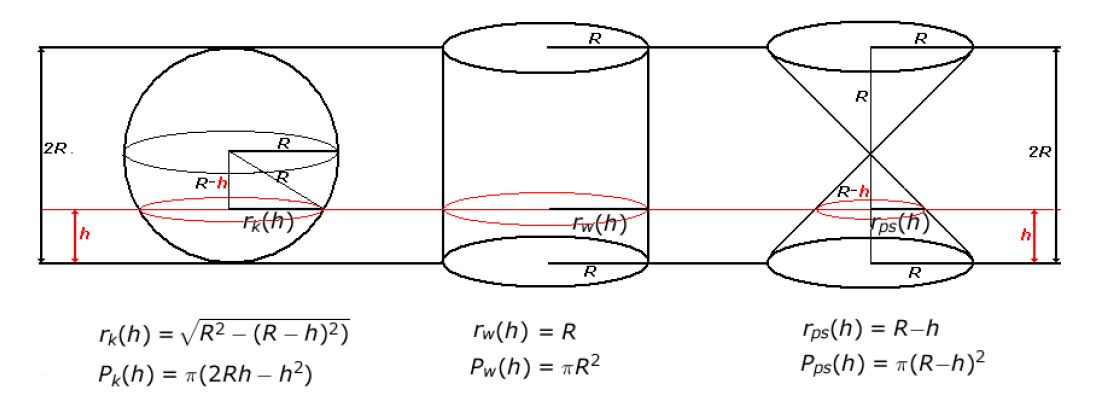 rysunek ilustruje sposób, w jaki Archimedes obliczył objętość kuli ponad 2200 lat temu
rysunek ilustruje sposób, w jaki Archimedes obliczył objętość kuli ponad 2200 lat temu
[C1] Jak całkowano na 100 lat przed wynalezieniem rachunku całkowego
Izabela Król,
"Obliczanie pól i objętości metodą Cavalieriego", praca magisterska, 2000.
plik pdf
Bonaventura Cavalieri to włoski matematyk żyjący w XVI wieku, a więc jakieś 100 lat przed
Newtonem i Leibnizem - wynalazcami rachunku różniczkowego i całkowego. Opracował sposoby
wyznaczania pól i objętości rozmaitych figur bardzo poglądową metodą, którą nazwał
metodą niepodzielnych. Nie było to ścisłe rozumowanie z punktu widzenia standardów
nowoczesnej matematyki, ale stało się szalenie popularne i modne, i było inspiracją także
dla Leibniza i Newtona. Niektóre elementy metody niepodzielnych dały się ująć w ścisłe reguły,
i są znane obecnie pod nazwą zasady Cavalieri'ego.
Omawiana tu praca poświęcona jest zaprezentowaniu głównych założeń zasady Cavalieri'ego,
oraz licznych obliczeń wykonanych przy pomocy tej zasady. Metoda jest tak poglądowa i przekonywująca,
że znakomicie nadaje się do spopularyzowania wśród miłośników geometrii. Ciekawe bryły, których
objętość wyznaczona jest w tej pracy, to m.in. torus (bryła w kształcie obwarzanka), elipsoida
obrotowa (patrz rysunek obok), a także wycinki paraboloid i hiperboloid obrotowych.
|
|
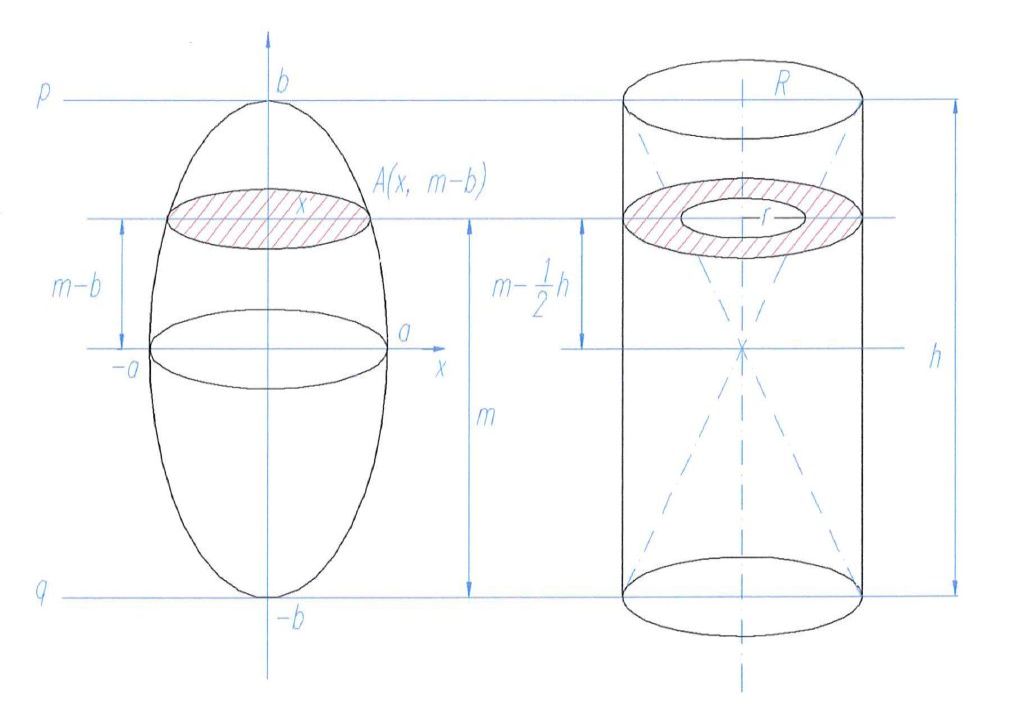 porównanie objętości elipsoidy obrotowej oraz wydrążonego walca - zgodnie z zasadą Cavalieri'ego
porównanie objętości elipsoidy obrotowej oraz wydrążonego walca - zgodnie z zasadą Cavalieri'ego
|
[C2] Cykloidy skrócone i wydłużone, oraz wyliczenie pola figur ograniczonych nimi i ich kierownicami
Agnieszka Kosmala,
"Obliczanie pól pewnych figur metodą Pascala i Archimedesa", praca magisterska, 2000.
plik pdf
W pracy zaprezentowane są linie zwane cykloidami, cykloidami skróconymi, oraz cykloidami wydłużonymi.
Są to linie utworzone przez punkty przyczepione do koła toczącego się po ustalonej prostej
(zwanej kierownicą tych cykloid). Liniami takim interesował się już w starożytności Archimedes,
zaś w XVII wieku słynny filozof i matematyk francuski Błażej Pascal przedstawił piękny sposób wyliczenia
pola figury ograniczonej cykloidą i jej kierownicą. Wyliczenie Pascala także zaprezentowane jest
w tej pracy, natomiast jej najciekawszą częścią jest wykorzystanie idei Pascala do podobnych
wyliczeń dla cykloid skróconych i wydłużonych. Zapoznanie się z tymi wyliczeniami nie wymaga
znajomości zaawansowanej matematyki - wystarczy matematyka szkolna.
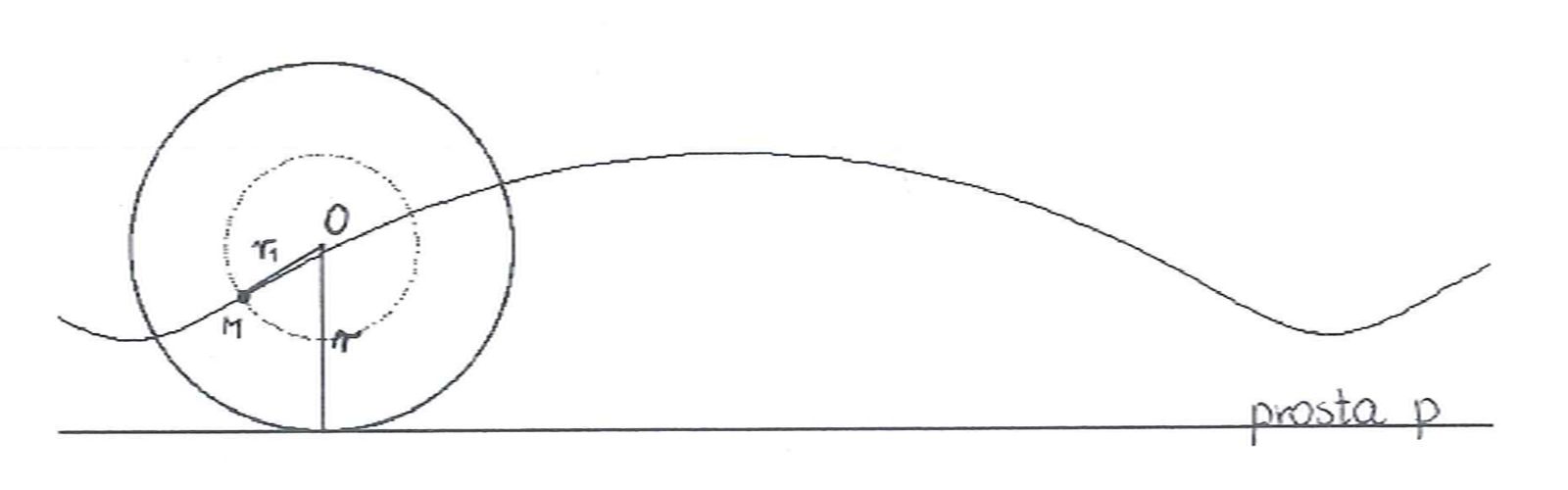
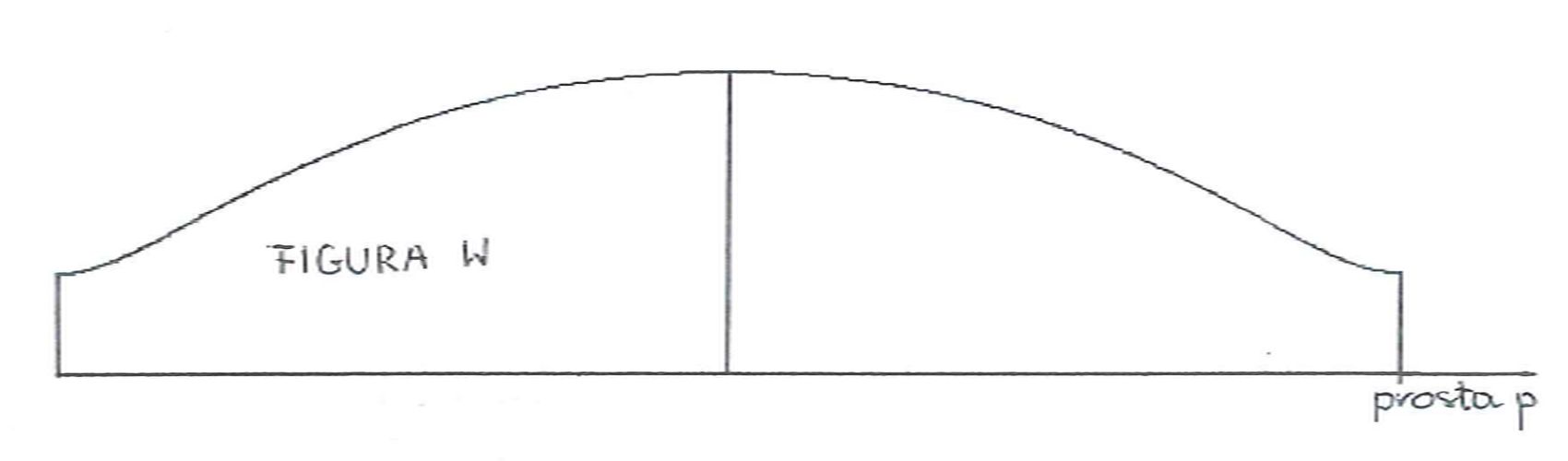
Rysunki poniżej przedstawiają kolejno: opis cykloidy skróconej (prosta p jest jej kierownicą),
figurę ograniczoną jednym cyklem
takiej cykloidy, oraz fragment rozumowania prowadzącego do obliczenia pola tej figury
z zastosowaniem zasady Cavalieri'ego - tak jak jest to opisane w pracy.
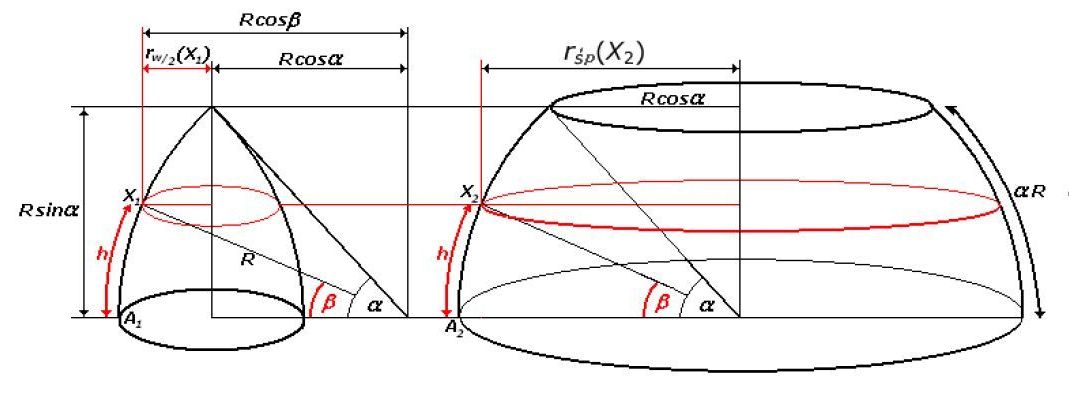
[C3] Wrzeciona, jabłka, obwarzanki - ich objętość i pole powierzchni
Bartłomiej Czerkas,
"Zastosowanie zasady Cavalieriego", praca magisterska, 2013.
plik pdf
Ta praca podejmuje raz jeszcze temat zasady Cavalieri'ego. Omówione są w niej rozmaite
dalsze warianty tej zasady, a także zaprezentowane rozmaite dalsze obliczenia, np.
wyznaczenie objętości wycinka hiperboloidy jednopowłokowej.
Najbardziej oryginalnym elementem tej pracy jest sformułowanie pewnego nowego wariantu
zasady Cavalieri'ego nadającego się szczególnie dobrze do wyliczeń pól powierzchni
brył obrotowych. Ten wariant zasady został w pracy wykorzystany m.in. do wyliczeń
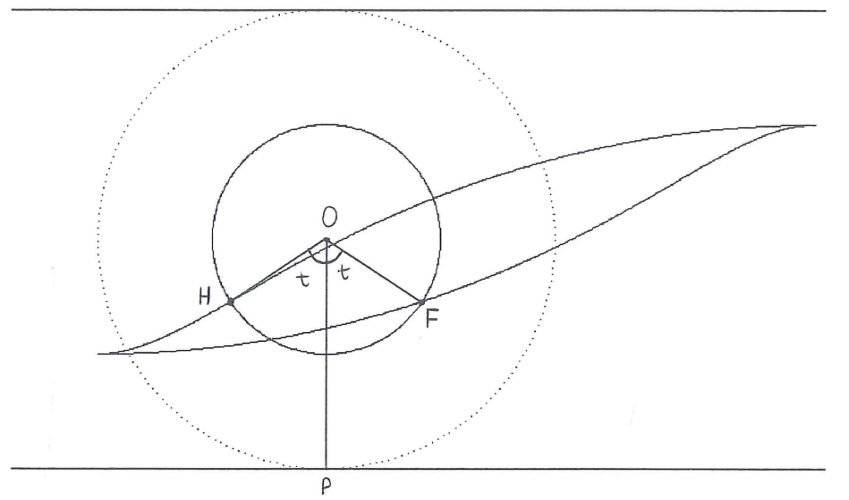
pól powierchni brył o kształcie wrzeciona (patrz rysunek obok), jabłka
(patrz Podrozdziały 3.6 i 4.5 w pracy), oraz obwarzanka (tzw. torus).
Rysunek obok przedstawia sposób zbudowania bryły obrotowej, którą nazywamy wrzecionem.
W pracy znajdują się wyliczenia objętości i pól powierzchni takich wrzecion, i wielu innych brył.
Do zrozumienia pracy nie potrzeba żadnej zaawansowanej wiedzy matematycznej - wystaczy dociekliwość i zdrowy rozsądek.
|
|
|
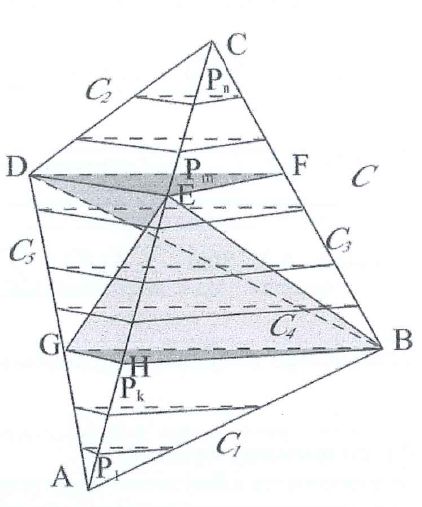
[C4] O "tomograficznym" wzorze na objętość
Magdalena Gapska,
"Objętość brył, których funkcja pola przekroju jest wielomianem conajwyżej trzeciego stopnia", praca magisterska, 2005.
plik pdf
Słowo "tomografia" pochodzi od greckiego słowa oznaczającego przekrój. Ma to tyle wspólnego z omawianą tu pracą,
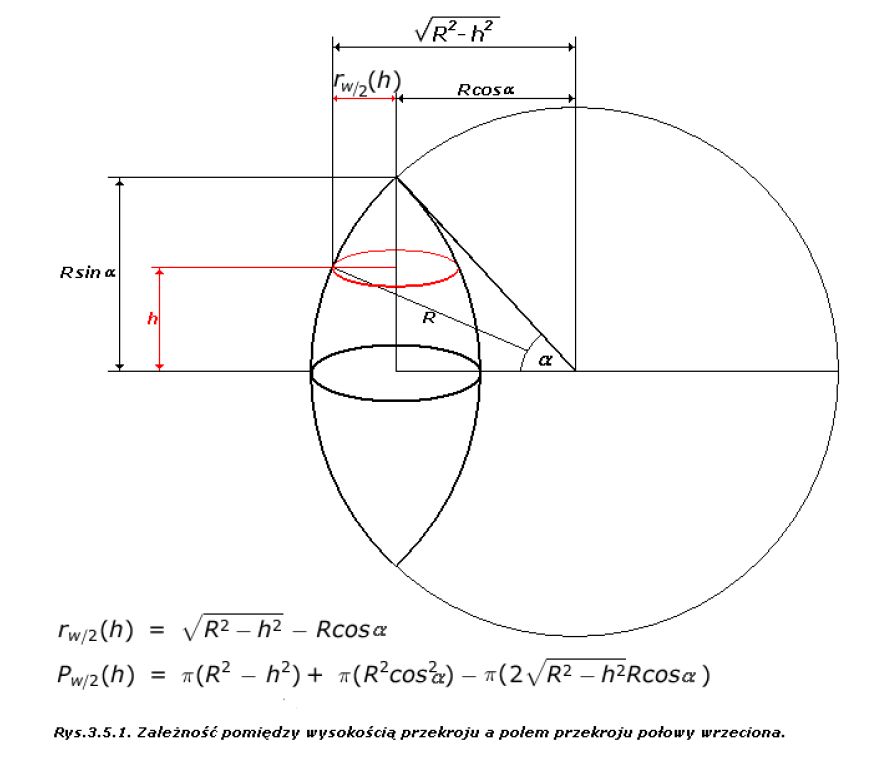
że jest w niej przedstawiony wzór na objętość wykorzystujący znajomość pól trzech przekrojów rozpatrywanej
bryły: przekrojów "górnego" i "dolnego", oraz przekróju "w połowie wysokości". Okazuje się, że wzór taki
jest poprawny dla zdumiewająco wielu brył, i dość przystępne uzasadnienie tego faktu znajdziecie w tej właśnie pracy.
Wspomniane uzasadninie będzie elementarne, i będzie wykorzystywać omawianą szeroko w innych pracach
z tego działu zasadę Cavalieri'ego.
Rysunek obok przedstawia dwie spośród naprawdę wielu brył,
do których można stosować omawiany w tej pracy wzór na objętość.
|
|
|
Dział 4: Pole figur na sferze i na płaszczyźnie nieeuklidesowej
Dwie zaprezentowane w tym dziale prace zawierają bardzo przystępne wprowadzenia do opartych na aksjomatach
teorii pola wielokątów na sferze i na płaszczyźnie nieeuklidesowej.
Druga praca, dotycząca płaszczyzny nieeuklidesowej, zawiera też zwięzłe i łatwo przyswajalne
wprowadzenie do tego, czym jest płaszczyzna nieeuklidesowa, oraz czym są podstawowe obiekty
geometryczne na tej płaszczyźnie.
|
|
|
[F1] Jak obliczać pole wielokątów na sferze?
Anna Grabowiecka,
"Teoria pola dla figur wielokątnych na sferze", praca magisterska, 2005.
plik pdf
Omawiana praca wprowadza w zagadnienie pola wielokątów na powierzchni sfery -
metodą aksjomatyczno-dedukcyjną.
Wielokąty sferyczne to figury ograniczone zamkniętymi łamanymi złożonymi
z segementów kół wielkich. Punktem wyjścia jest założenie, że pole całej sfery
wynosi 4π. Potem następuje wyznaczenie pół tzw. dwukątów sferycznych,
czyli figur o kształcie ograniczonym dwoma południkami.
To prowadzi następnie do wzoru na pole sferycznych trójkątów.
Okazuje się, że pole dowolnego sferycznego trójkąta jest równe
nadwyżce jego sumy kątów ponad π (czyli ponad wartość sumy kątów dla dowolnego
trójkąta na zwykłej płaszczyźnie). Kolejny krok polega na uogólnieniu
tej obserwacji na dowolne wielokąty sferyczne.
W dalszej części praca zawiera analizę teorii pola dla wielokątów sferycznych
pod kątem jej niesprzeczności (czyli logicznej koherentności), oraz pod kątem
tego, czy poszczególne aksjomaty są w tej teorii niezbędne (dokładniej, wykazana
jest niezależność każdego z aksjomatów od pozostałych). Dzięki temu teoria ta
nabiera statusu porządnej matematycznej teorii.
W dodatkowym końcowym razdziale pracy zaprezentowane jest
wyliczenie pola czaszy sferycznej, jako granicy pól wielokątów wpisanych w tą czaszę.
|
|
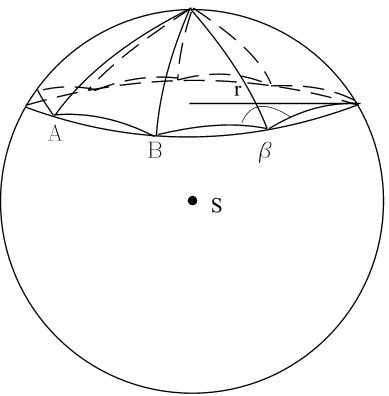
Wielokąt sferyczny wpisany w czaszę sfery. Pole czaszy zostało w pracy obliczone jako granica
pól takich wielokątów sferycznych.
|
[F2] Czym jest pole wielokątów w geometrii nieeuklidesowej?
Justyna Zakręt,
"Pojęcie pola w geometrii nieeuklidesowej", praca magisterska, 2005.
plik pdf
Praca zaczyna się od zwięzłego wytłumaczenia czym jest płaszczyzna nieeuklidesowa.
Następnie zaprezentowane są aksjomaty (czyli podstawowe własności), na których oparta jest
teoria pola wielokątów na płaszczyźnie nieeuklidesowej. Wszystkie podstawowe własności pola,
i wzory, wyprowadzone są metodą dedukcji z przedstawionych aksjomatów. Opis jest bardzo przystępny.
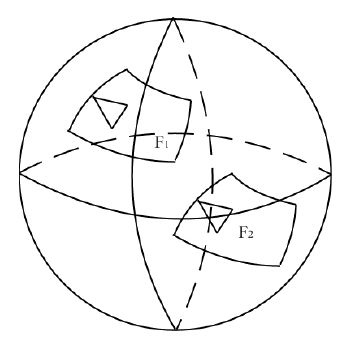
Najciekawszy wyprowadzony fakt mówi, że pole nieeuklidesowego n-kąta można obliczyć
za pomocą miar jego kątów: jest ono równe tzw. defektowi, czyli różnicy pomiędzy
sumą kątów w dowolnym n-kącie euklidesowym oraz sumą kątów danego nieeuklidesowego
n-kąta.
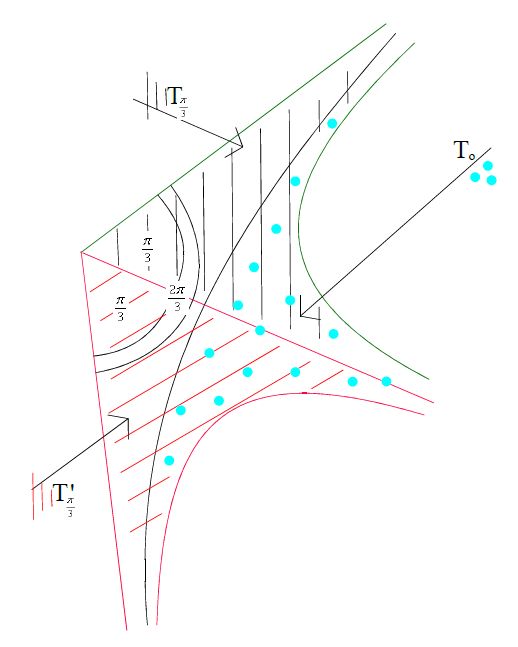
Ciekawym fenomenem w geometrii nieeuklidesowej jest istnienie figur bardzo przypominających
wielokąty, które są nieograniczone, ale mają skończone pole. Są to tzw.
wielokąty idealne. Praca zawiera omówienie również takich wielokątów idealnych,
wyjaśnienie jak to jest
możliwe, by miały skonczone pole, a także uogólnienia pojęcia defektu, i wzorów na pole,
które stosują się także do takich wielkątów.
Ostatnia część pracy zawiera poglądową i ścisłą analizę przedstawionej teorii
pod kątem jej logicznej niesprzeczności, oraz pod kątem niezależności jej aksjomatów.
|
|
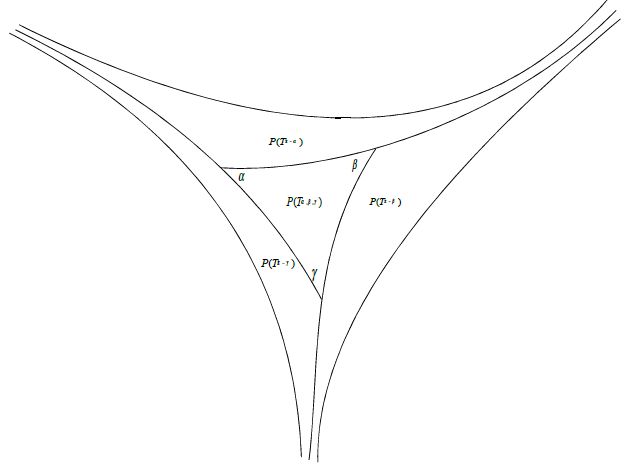
Rysunek ilustruje sposób dowodu faktu, że pole trójkąta nieeuklidesowego jest równe jego defektowi.
|
Dział 5: Równoważność przez rokład a równość pól lub objętości
Rozcinanie figur na części, i składanie z tych części innych figur, to bardzo wdzięczne źródło
zagadek i łamigłówek, by wspomnieć tylko o znanych układankach takich jak PENTOMINO czy TANGRAM.
Jednak zagadnienie to ma też głębszą treść, poprzez swój związek z pojęciem pola. Dla starożytnych
geometrów greckich był to podstawowy sposób porównywania wielkości figur. Zebrane w tym dziale
teksty opracowań zawierają omówienie rozmaitych aspektów tego zagadnienia.
Praca
[R1]
jest tekstem podstawowym, w którym starannie omówione jest pojęcia
równoważności przez rozkład, polegające właśnie na możliwości rozłożenia figury na części,
i złożenia z nich drugiej figury. Praca zawiera też przystępny dowód niebanalnego faktu,
że dowolne dwa wielokąty o równych polach są równoważne przez rozkład.
Od około 120 lat wiadomo, że analogiczny fakt nie ma miejsca dla wielościanów o jednakowych
objętościach, przynajmniej nie w pełnej ogólności. W pracy
[R2]
pokazane jest jednak,
że dowolne dwa graniastosłupy mające tą samą objętość są równoważne przez rozkład
(ten sam fakt jest też wyjaśniony, nieco inaczej, w Rozdziale 5.2 pracy
[R1]).
Praca
[R3]
omawia zagadnienie równoważności przez rozkład w geometrii nieeuklidesowej.
Ostatnia praca
[R4]
dotyczy natomiast pojęcia translacyjnej równoważności przez rozkład,
gdzie w procesie rozkładania i składania figur,
poszczególnych ich części nie można obracać, lecz jedynie przesuwać.
|
|
|
[R1] O rozcinaniu figur na części i składaniu z tych części innych figur
Krzysztof Godzwon,
"Równoważność przez rozkład dla wielokątów i wielościanów", praca magisterska, 1999.
plik pdf
Omawiana praca zawiera wszechstronne i przystępne wprowadzenie do pojęcia równoważności
przez rozkład dla wielokątów i wielościanów. Rozdział 2 zawiera opis pojęcia równoważności
przez rozkład dla wielokątów, oraz wyprowadzenie podstawowych własności tego pojęcia.
Rozdział 3 wyjaśnia jak można użyć pojęcia równoważności przez rozkład do ścisłego
zdefiniowania pojęcia pola. Rozdział 4 zawiera dowód dość zdumiewającego twierdzenia
Bolyai-Gerwiena: dowolne dwa wielokąty o równych polach są równoważne przez rozkład.
Rozdział 5 zawiera omówienie równoważności przez rozkład dla wielościanów. Tu sytuacja jest inna niż
dla wielokątów, gdyż nie każde dwa wieloścany o jednakowych objętościach są równoważne przez rozkład.
Ten dość trudny fakt nie jest wprawdzie udowodniony w pracy, ale jest on
dość ciekawie i wyczerpująco skomentowany. Przykładowo, Podrozdział 5.2
zawiera analizę równoważności przez rozkład dla graniastosłupów, a jego zwieńczeniem jest
pokazanie, że każde dwa graniastosłupy o równych objętościach są równoważne przez rozkład.
Z kolei Podrozdział 5.3 zawiera opis pewnego sposobu rozstrzygania, że dwa wielościany nie są
równoważne przez rozkład, oraz zastosowanie tego sposobu do wykazania, że czworościan
foremny nie jest równoważny przez rozkład z jakimkolwiek prostopadłościanem. Pokazane są też
przykłady innych czworościanów, które są równoważne przez rozkład z prostopadłościanami.
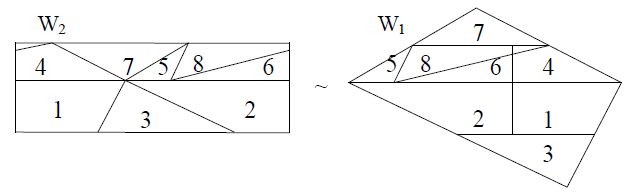
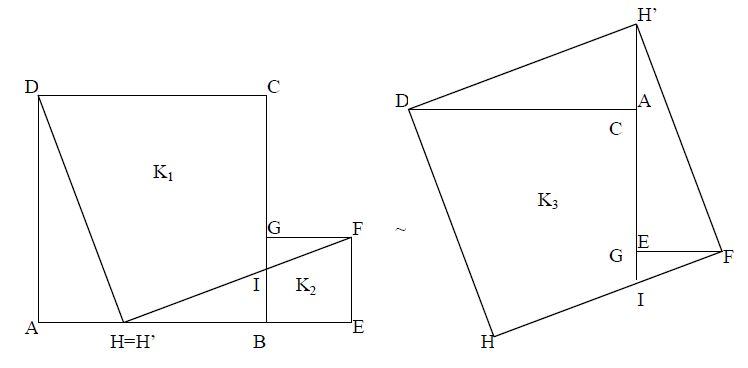
Rysynek po lewej ilustruje pojęcie równoważności przez rozkład. Rysunek po prawej dowodzi, że kwadrat
zbudowany na przeciwprostokątnej trójkąta prostokątnego jast równoważny przez rozkład z sumą dwóch
kwadratów zbudowanych na przyprostokątnych - jest to słynne twierdzenie Pitagorasa w wersji,
w jakiej odkrył je Pitagoras.
[R2] Rozkład na wspólne części dla dowolnych dwóch graniastosłupów (także pochyłych) o równych objętościach
Beata Zwierzańska,
"Równoważność przez rozkład dla graniastosłupów" , praca magisterska, 2005.
plik pdf
W pracy omówiony jest 3-wymiarowy wariant pojęcia równoważności przez rozkład - dla wielościanów.
Dość znane twierdzenie mówi, że inaczej jak w przypadku 2-wymiarowym, nie każde dwa wielościany
o tej samej objętości są równoważne przez rozkład. (Przykładowo, czworościan foremny i sześcian
o tej samej objętośc i nie są równoważne przez rozkład.) Mniej znay jest fakt, że dla dużej
rodziny wielościanów równośc objętości wystarcza do tego by były równoważne przez rozkład.
Tak jest np. dla dowolnych dwóch graniastosłupów, choćby nawet pochyłych.
Uzasadnienie tego właśnie faktu jest głównym celem opisywanej tu pracy.
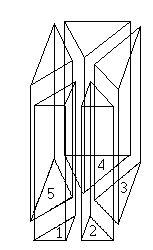
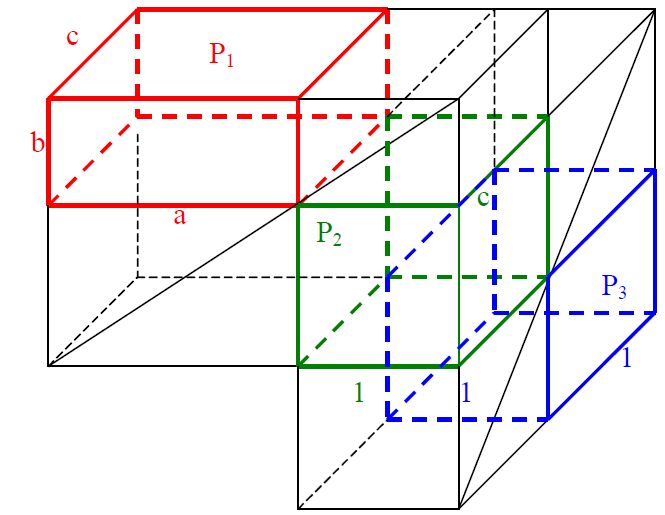
Rysunek obok ilustruje
jedną z pomocniczych obserwacji poczynionych w pracy, a mianowicie:
każdy prostopadłościan jest równoważny przez rozkład z sześcianem.
|
|
|
[R3] Rozcinanie i ponowne zestawianie figur na płaszczyźnie nieeuklidesowej
Karolina Tomaszewska,
"Równoważność przez rozkład figur w geometrii nieeuklidesowej" , praca magisterska, 2005.
plik pdf
Czy znany ze zwykłej geometrii fakt, że dowolne dwa wielokąty o jednakowych polach są równoważne przez rozkład,
zachodzi także w geometrii nieeuklidesowej? Okazuje się, że tak! Przystępny sposób wyjaśnienia tego zjawiska
znajduje się w opisywanej tu pracy. Czytelnik nie musi nawet wiedzieć co to takiego ta geometria nieeuklidesowa.
Pierwsza część pracy zawiera zwięzłe opisanie czym jest płaszczyzna nieeuklidesowa, na tyle wyczerpujące,
że z jego pomocą wszystkie dalsze rozważania można śledzić bez wcześniejszej znajopmości geometrii nieeuklidesowej.
Praca jest pod tym względem samowystarczalna.
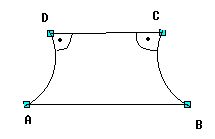
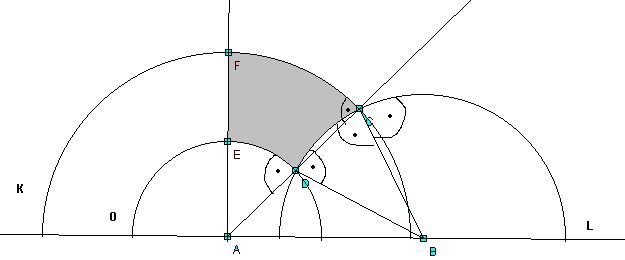
Czworokąt Saccheri'ego to figura w geometrii nieeuklidesowej nieco podobna do równoramiennego trapezu
mającego dwa kąty proste przy krótszej podstawie, i dwa ostre przy dłuższej. Rysunek po lewej przedstawia
schematyczny wygląd pewnego czworokąta Saccheri'ego, zaś rysunek po prawej przedstawia taki czworokąt
w odwzorowaniu (modelu) półpłaszczyznowym Poincare'go płaszczyzny nieeuklidesowej. Analiza czworokątów
Saccheri'ego stanowi kluczowe narzędzie w pracy pozwalające uzasadnić, że dowolne dwa nieeuklidesowe
wielokąty o jednakowych polach są równoważne przez rozkład.
[R4] Rozcinanie i zestawianie nowych wielokątów bez obracania części
(części można tylko przesuwać)
|
Anna Koch,
"Równoważność translacyjna figur wielokątnych" , praca magisterska, 2006.
plik pdf
Dwie figury umieszczone na płaszczyźnie są translacyjnie równoważne przez rozkład
jeśli pierwszą z nich można podzielić na części A_1, A_2, ... , A_n zaś drugą na części
B_1, B_2, ... , B_n w taki sposób, że każda część B_i jest przesuniętą (przez pewną translację)
kopią części A_i.
Oczywiście każda figura jest translacyjnie równoważna przez rozkład z dowolną swoją przesuniętą kopią,
ale już nie jest jasne czy np. kwadrat i jego lekko obrócona kopia są równoważne przez rozkład
(z analizy przedstawionej w pracy wynika, że jest to prawda!).
W opisywanej tu pracy podany jest przystępny sposób na szybkie rozstrzygnięcie czy dwie figury
na płaszczyźnie są translacyjnie
równoważne przez rozkład, czy nie. Odpowiedź wcale nie jest oczywista!
|
|
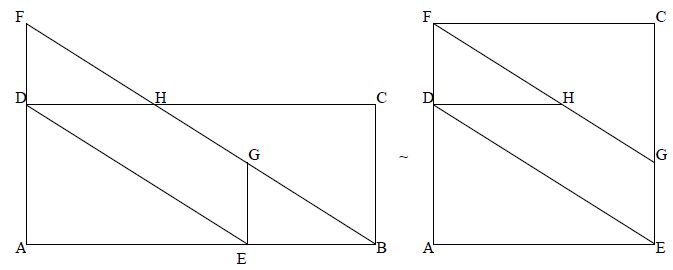
rysunek ilustruje fakt, że dowolny prostokąt jest translacyjnie rónoważny
przez rozkład z kwadratem o bokach równoległych do boków tego prostokąta
|